Thể loại: Bài viết nổi bật » Thợ điện Novice
Số lượt xem: 92355
Bình luận về bài viết: 1
Đại số Boolean. Phần 2. Các luật và chức năng cơ bản
 Tiếp tục câu chuyện về đại số Boolean, quy ước, quy tắc, phép toán. Chuyển đổi sang cơ bản của các mạch tiếp xúc.
Tiếp tục câu chuyện về đại số Boolean, quy ước, quy tắc, phép toán. Chuyển đổi sang cơ bản của các mạch tiếp xúc.
Trong bài viết đầu tiên George Bull được mô tả là người tạo ra đại số của logic. Bài viết thứ hai sẽ mô tả các hoạt động cơ bản của đại số Boolean và các phương pháp để đơn giản hóa các biểu thức Boolean. Vì vậy, đại số Boolean sử dụng các câu lệnh làm đối số, và không phải ý nghĩa của chúng, mà là sự thật hoặc giả dối của câu lệnh.
Các hình thức để viết biểu thức trong đại số Boolean.
Nếu tuyên bố là đúng, thì nó được viết như sau: A = 1, nếu nó sai, thì A = 0 (xét cho cùng, không đúng là khoai tây là một loại trái cây). Đối với bất kỳ câu lệnh nào, A là true (A = 1) hoặc false (A = 0). Không thể có trung gian ở đây. Chúng tôi đã nói về điều này.
Nếu bạn kết nối hai câu lệnh đơn giản với liên minh Và, bạn sẽ nhận được một câu lệnh phức tạp, được gọi là một sản phẩm hợp lý. Chúng ta hãy nói hai câu đơn giản: Ba Ba nhiều hơn hai người, chúng tôi sẽ chỉ định bằng chữ A, Ba ít hơn năm - - bằng chữ B.
Do đó, câu lệnh phức tạp, Three Three nhiều hơn hai và ít hơn năm năm là một logic hợp lý (trong trường hợp này là chữ in hoa và, nói rằng đây là một hoạt động logic logic và, cũng như sau này trong văn bản. và B. Nó được chỉ định như sau: A ^ B hoặc A * B.
Phép nhân logic (thao tác "VÀ").
Trong đại số sơ cấp A * A = A2. Nhưng trong đại số Buhlùi A * A = A2 = A, A * A = A, vì dấu nhân (*) bây giờ có nghĩa là ... Và ... theo nghĩa của Và ... Và. Tất cả kinh nghiệm của chúng tôi xác nhận rằng A & A giống như A. một mình. Người ta không thể không đồng ý với điều này. Sự thật của tuyên bố không thay đổi nếu nó được lặp lại bởi yếu tố nhiều lần.
Sản phẩm của hai câu lệnh được coi là đúng (bằng 1), sau đó, và chỉ khi cả hai yếu tố đều đúng và sai (bằng 0) nếu ít nhất một trong các yếu tố là sai. Đồng ý rằng các quy tắc này không mâu thuẫn với lẽ thường, và, ngoài ra, chúng hoàn toàn tuân thủ các quy tắc của đại số sơ cấp:
1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.
Bình đẳng đầu tiên đọc như sau: nếu cả A và B đều đúng, thì sản phẩm A * B là đúng. Trong đại số Buhl, dấu nhân (*) thay thế liên kết I.
Các sản phẩm hợp lý có thể bao gồm không phải hai, nhưng số lượng báo cáo lớn hơn - các yếu tố. Và trong trường hợp này, sản phẩm chỉ đúng khi cùng lúc tất cả các yếu tố tuyên bố là đúng.
Bổ sung logic (HOẶC hoạt động)
Nếu hai câu được kết nối bởi một liên minh HOẶC. câu ghép được hình thành đó được gọi là tổng hợp logic.
Hãy xem xét một ví dụ về một tổng hợp logic. Nói A: "Hôm nay tôi sẽ đi xem phim."
Tuyên bố B: Hôm nay tôi sẽ đi đến sàn nhảy. Chúng tôi thêm cả hai tuyên bố và nhận được: "Hôm nay tôi sẽ đi xem phim HOẶC vào một sàn nhảy."
Câu lệnh phức tạp này được ký hiệu như sau: A + B = C hoặc (A V B) = C.
Bằng C, chúng tôi biểu thị một tuyên bố phức tạp của một tổng hợp logic.
Trong ví dụ đang xem xét, liên minh HOẶC không thể được sử dụng theo nghĩa độc quyền. Thật vậy, trong cùng một ngày bạn có thể đến rạp chiếu phim và đến sàn nhảy. Và đây là câu nói:
Chủ tịch của quan hệ đối tác làm vườn sẽ là Petrov hoặc Ivanov, không phải là một tổng hợp logic, bởi vì chỉ có một người sẽ là chủ tịch, và người còn lại sẽ là một người làm vườn bình thường nghiệp dư.
Dấu V cho tổng hợp logic được chọn vì đó là chữ cái đầu của từ Latin "vel", có nghĩa là "hoặc", trái ngược với từ Latin "aut>, có nghĩa là" và ". Bây giờ nó phải rõ ràng cho mọi người tại sao sản phẩm hợp lý được biểu thị bằng dấu hiệu ^.
Trong đại số sơ cấp có quy tắc A + A = 2A. Quy tắc này là đúng, bất kể số nào được biểu thị bằng chữ A. Trong đại số Boolean, quy tắc A + A = A tương ứng với nó. Kinh nghiệm toàn bộ cuộc sống của chúng tôi nói rằng nói A HOẶC hoặc cả A chỉ là một cách khác và dài hơn để nói chỉ A.
Giống như bất kỳ câu lệnh ghép nào, tổng của hai câu A và B có thể đúng hoặc sai. Tổng được coi là đúng, nghĩa là bằng với sự thống nhất, nếu ít nhất một trong các điều khoản là đúng:
A + B = 1 nếu OR A = 1 HOẶC B = 1, phù hợp với số học thông thường:
1+0 = 0+1 = 1.
Nếu cả hai câu lệnh tổng hợp đều đúng, thì tổng cũng được coi là đúng, do đó, trong đại số Boolean, chúng ta có: (1) + (1) = 1.
Các dấu ngoặc được đặt ở đây để nhấn mạnh điều kiện, ý nghĩa của phép cộng này và không phải là số học.
Tổng của hai câu lệnh được coi là sai và bằng 0 nếu, nhưng chỉ khi cả hai thuật ngữ đều sai. Từ đây:
0 + 0=0.
Vì vậy, tổng của hai câu A + B được coi là đúng nếu đúng, HOẶC A, HOẶC B, HOẶC cả hai thuật ngữ cùng nhau. Do đó, từ OR được ký hiệu là +.
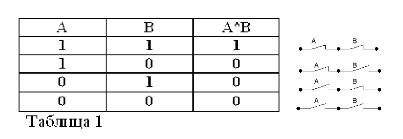
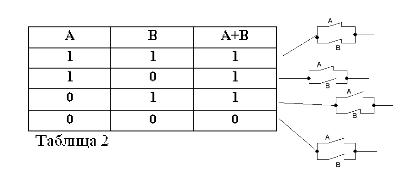
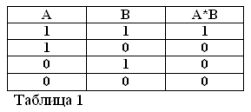
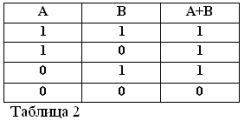
Hãy nhớ rằng các câu A và B chỉ có thể đúng hoặc sai và do đó, có thước đo về sự thật 1 hoặc 0, kết quả của các phép toán AND và OR được xem xét có thể được tóm tắt trong bảng 1 và 2.
Hoạt động thứ ba, được sử dụng rộng rãi bởi đại số Buhl, là hoạt động phủ định - KHÔNG. Chúng tôi nhắc nhở bạn rằng đại số sơ cấp sử dụng các phép toán ADD, D Subtract, Nhân với, Chia cho và một số khác.
Đối với mỗi câu A, có phủ định KHÔNG phải A, mà chúng ta sẽ biểu thị bằng ký hiệu / A. Điều này không nên nghi ngờ.
Chúng tôi đưa ra ví dụ: chúng tôi sẽ đi vào rừng
Nếu tuyên bố A là đúng, nghĩa là A = 1, thì phủ định của nó / A phải sai / A = 0. Và ngược lại, nếu bất kỳ tuyên bố nào là sai, thì phủ định của nó là đúng. Ví dụ: Một con ngựa không ăn hay Hay / A = 0, Một con ngựa không ăn hay hay (A = 1). Điều này có thể được thể hiện trong bảng 3.
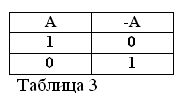
Xác định ý nghĩa của hành động phủ định và giả sử rằng hai câu A và / A luôn luôn đúng, hai công thức mới của đại số Boolean tuân theo:
A + (/ A) = 1 và A * (/ A) = 0.
Ngoài ra còn có các công thức khác giúp đơn giản hóa việc xử lý logic của các câu lệnh. Ví dụ: 1 + A = 1, vì theo định nghĩa của phép cộng, trong trường hợp khi một số hạng bằng với đơn vị, tổng luôn luôn bằng với đơn vị. Kết quả thu được không phụ thuộc vào việc A = 0 hay A = 1.
Mỗi trong số ba phép toán logic mà chúng tôi đã kiểm tra (AND, OR, KHÔNG) có các thuộc tính nhất định gần với quy tắc của đại số sơ cấp. Nếu tất cả chúng được xây dựng, thì chúng ta có 25 quy tắc của đại số Boolean. Chúng khá đủ để giải quyết hầu hết mọi vấn đề logic. Không có các quy tắc này, việc giải quyết các vấn đề logic trở nên khá khó khăn vì sự phức tạp rõ ràng của chúng. Cố gắng tìm câu trả lời chính xác mà không sử dụng các quy tắc có nghĩa là thay thế chúng bằng sự khéo léo và lý luận chung. Các quy tắc rất thuận lợi cho công việc này và tiết kiệm thời gian.
Trong khuôn khổ của bài viết, không thể xem xét tất cả 25 quy tắc này, nhưng những người muốn luôn có thể tìm thấy chúng trong các tài liệu liên quan.
Như đã đề cập trong bài báo đầu tiên vào năm 1938, nhà khoa học trẻ người Mỹ Claude Shannon trong bài viết của ông Cốt truyện Phân tích Rơle và Mạch chuyển mạch Lần đầu tiên sử dụng đại số Boolean cho các vấn đề về công nghệ chuyển tiếp. Khám phá của Shannon là ông nhận ra rằng phương pháp thiết kế máy chuyển tiếp và máy tính điện tử thực sự là một nhánh của logic toán học.
Nó thường xảy ra. Trong nhiều năm, nhà khoa học đã nghiên cứu một vấn đề dường như hoàn toàn không cần thiết đối với đồng bào của mình - chỉ là niềm vui. Nhưng nhiều thập kỷ và đôi khi nhiều thế kỷ trôi qua, và một lý thuyết mà không ai cần không chỉ có được quyền tồn tại, mà không có nó thì tiến bộ hơn nữa trở nên không thể tưởng tượng được.
Điều gì đã giúp Shannon lần thứ hai khám phá ra đại số Boolean? Trường hợp nào? Không có gì của các loại.
Tình yêu của các máy chuyển tiếp, được chế tạo trên các công tắc và rơle thông thường, đã giúp nhà khoa học trẻ kết nối một lý thuyết bị lãng quên với các nhiệm vụ trao đổi điện thoại tự động, lúc đó ông làm việc. Sau đó, Shannon đưa ra ý tưởng tương tự về việc có hoặc không có những thông điệp riêng biệt và đặt nền tảng cho toàn bộ phần của điều khiển học - lý thuyết thông tin.
Đại số của Buhl rất phù hợp để phân tích và tổng hợp các mạch chuyển tiếp. Như vậy là đủ để chấp nhận như một tuyên bố đúng: Có một tín hiệu trong mạch, và là một tín hiệu sai - Tử Không có tín hiệu nào trong mạch, khi một đại số mới xuất hiện - đại số tín hiệu, đại số mạch chuyển tiếp.
Đại số mới chỉ có giá trị cho việc xem xét các mạch chuyển tiếp và chuyển mạch. Rốt cuộc, chỉ trong những sơ đồ như vậy là điều kiện có một tín hiệu và không có tín hiệu nào được thỏa mãn. Trong trường hợp tín hiệu thay đổi liên tục, có được một số lượng lớn các điều kiện trung gian tùy ý (tín hiệu đó được gọi là tương tự), đại số rơle không được áp dụng. Điều này phải luôn được ghi nhớ. Nhưng chỉ phần lớn các máy tính điện tử và máy từ tính sử dụng nguyên tắc xử lý tín hiệu riêng biệt, dựa trên các yếu tố có, có - không.
Biểu thức mà Liên hệ đóng kín đã được Shannon chấp nhận là đúng (1), và Liên hệ mở ra là sai (0). Phần còn lại của "đại số", bao gồm các phép toán AND, OR và NOT và 25 quy tắc, Shannon đã mượn từ Boole.
Đại số mạch chuyển tiếp hóa ra đơn giản hơn đại số Boolean, vì nó chỉ liên quan đến các phần tử của loại "có - không". Ngoài ra, đại số mới là trực quan hơn.
Các yếu tố trong đại số này là các liên hệ, mà chúng ta sẽ biểu thị bằng các chữ cái A, B, C ... Liên hệ được đóng - A, liên hệ được mở - / A (chữ có dấu gạch ngang).
Ký hiệu, như bạn thấy, hoàn toàn được lấy từ đại số Boolean. Một liên hệ mở là một phủ định của một liên hệ kín. Liên hệ tương tự không thể được đóng và mở.
Chúng ta hãy đồng ý rằng nếu trong bất kỳ mạch nào, hai tiếp điểm được biểu thị bằng cùng một chữ cái, điều này có nghĩa là chúng luôn lấy cùng một giá trị.
Tại bất kỳ thời điểm nào, cả hai đều mở cùng một lúc hoặc cả hai đều đóng. Cách dễ nhất để tưởng tượng chúng được kết nối cơ học với nhau để cả hai cùng lúc mở hoặc đóng.
Nếu trong một chuỗi nào đó một liên hệ là một phủ định của một liên hệ khác, thì ý nghĩa của chúng luôn luôn ngược lại. Ví dụ: các liên hệ C và / C không bao giờ có thể được mở đồng thời hoặc đóng đồng thời. Và trong sơ đồ, chúng có thể được biểu diễn kết nối một cách cơ học: nếu một trong số chúng mở ra, thì cái kia đóng lại.
Chúng ta bắt đầu làm quen với đại số chuyển tiếp bằng cách phân tích các mạch đơn giản nhất tương ứng với các hoạt động AND, OR và KHÔNG.
Tích của hai tiếp điểm (hoạt động AND) là mạch thu được do kết nối chuỗi của chúng: nó chỉ được đóng (bằng 1) khi cả hai tiếp điểm được đóng (bằng 1).
Tổng của hai tiếp điểm (hoạt động OR) sẽ là mạch được hình thành khi chúng được kết nối song song: nó được đóng (bằng 1) khi có ít nhất một trong các tiếp điểm tạo thành mạch được đóng (bằng 1).
Đối diện của liên hệ này (hoạt động KHÔNG) là một liên hệ bằng 0 (mở) nếu liên hệ này là 1 (đóng) và ngược lại.
Như trong đại số Boolean, nếu các tiếp điểm được biểu thị bằng các chữ cái A và B, thì chúng ta sẽ biểu thị tích của hai liên hệ bằng A * B, tổng của A + B và tiếp điểm đối diện A, bởi / A. Ở trên được giải thích trong Hình 1, 2 và 3.
Hiệu lực của các bảng tương ứng với các hoạt động AND, OR và KHÔNG. bây giờ không ai nên nghi ngờ
Hãy để chúng tôi tập trung vào hai ví dụ: 1 * 0 = 0 và 1 + 0 = 1.
Có thể thấy trong hình rằng một liên hệ đóng vĩnh viễn được kết nối nối tiếp với một liên hệ mở liên tục tương đương với một liên hệ mở vĩnh viễn (1 * 0 = 0) Một liên hệ đóng vĩnh viễn được kết nối song song với một liên hệ mở liên tục tương đương với một liên hệ đóng vĩnh viễn.
Khi đã làm quen với số học của các mạch tiếp xúc, bạn có thể mô tả bất kỳ mạch chuyển tiếp nào bằng một công thức sử dụng các quy ước được chấp nhận. Trong điều khiển học, các công thức như vậy được gọi là cấu trúc.
Nếu công thức cấu trúc của bất kỳ mạch chuyển tiếp nào là 1, thì tín hiệu có thể đi qua nó - mạch bị đóng. Và ngược lại, nếu công thức cấu trúc của mạch bằng 0, tín hiệu sẽ không đi qua nó - mạch bị hỏng.Kết luận: hai mạch chuyển tiếp tương đương với nhau khi công thức cấu trúc của chúng bằng nhau.
Trong phần tiếp theo của bài viết, chúng tôi sẽ xem xét các ví dụ về mạch tiếp xúc, mạch tiếp xúc điển hình và tương đương của chúng, cũng như vẽ sơ đồ theo các công thức cấu trúc. Chúng tôi cũng xem xét các mạch logic chính thực hiện các chức năng của đại số Boolean.
Tiếp tục bài viết: Đại số Boolean. Phần 3. Đề án liên hệ
Boris Aladyshkin
Xem thêm tại electro-vi.tomathouse.com
: