Đại số Boolean. Phần 1. Một chút lịch sử

Ở trường, tất cả chúng ta đều học đại số, nhưng họ không nói về đại số Boolean ở đó. Sự khác biệt giữa đại số Boolean và đại số trường học, lịch sử xuất hiện, các vấn đề và ứng dụng của nó được mô tả trong bài viết này.

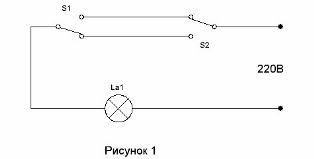
Mạch cho phép hai công tắc bật đèn trong hành lang ở lối vào hành lang và tắt khi vào phòng đã được biết đến từ rất lâu (xem. Mạch điều khiển chiếu sáng hành lang). Nó được hiển thị trong Hình 1.

Nhiệm vụ số 1. Phức tạp hơn. Tạo một sơ đồ cho phép bạn bật và tắt đèn trong phòng bằng bất kỳ 3 công tắc khác nhau. Công tắc được đặt ở lối vào phòng, phía trên giường và tại bàn làm việc.

Nhiệm vụ số 2.

Trong một ủy ban thể thao, chẳng hạn như một ủy ban nhà máy, 5 thẩm phán đã tập hợp.

Mỗi người trong số họ phải bỏ phiếu cho các quyết định khác nhau. Quyết định được thông qua bởi đa số phiếu bầu, nhưng chỉ với điều kiện bổ sung là chủ tịch ủy ban bỏ phiếu cho nó.

Các thẩm phán bỏ phiếu bằng cách nhấn nút đóng công tắc nằm dưới bàn mà họ đang ngồi. Đóng công tắc, họ bỏ phiếu ủng hộ, ngắt kết nối các khuyết điểm. Vẽ một sơ đồ đơn giản cho phép bạn tự động xem kết quả bỏ phiếu. Trong trường hợp đơn giản nhất, chỉ cần với sự trợ giúp của bóng đèn - sáng lên - quyết định đã được đưa ra, không sáng lên - không.

Nhiệm vụ số 3. Trong thực tế, điều này là không thể, nhưng vì một nhiệm vụ giáo dục phức tạp là khá phù hợp.

Trong một căn phòng hình lục giác lớn, một công tắc được lắp đặt trên mỗi bức tường. Xây dựng một mạch để bất cứ lúc nào bạn có thể bật hoặc tắt đèn trong phòng bằng cách bật một (bất kỳ) công tắc.

Sau khi bạn không thành công trong các nhiệm vụ trong ba đến bốn ngày, hãy tạm thời đặt chúng sang một bên. Và bận rộn Đại số Boolean. Đó là đại số Boolean, hay, vì nó cũng được gọi là, Đại số Boolean, đại số mạch chuyển tiếp, sẽ giúp bạn giải quyết vấn đề của bạn.

Đại số Boolean là gì?

Thật kỳ lạ, mặc dù thực tế là trong năm năm họ đã học đại số ở trường, nhiều học sinh và người lớn sau này sẽ không thể trả lời câu hỏi, đại số là gì? Đại số là một khoa học nghiên cứu tập hợp một số yếu tố và hành động trên chúng.

Trong một khóa học ở trường đại số, các yếu tố như vậy là những con số. Các con số có thể được biểu thị không phải bằng số, mà bằng chữ cái, mọi người đều quen thuộc với điều này. Trong những bài học đầu tiên về đại số, điều này luôn gây khó khăn cho nhiều học sinh. Hãy nhớ rằng ban đầu khó khăn như thế nào để làm quen với việc thêm chữ cái thay vì số, giải các phương trình không nói gì.

Có lẽ, mỗi người trong chúng ta sau đó đã tự hỏi mình câu hỏi: Tại sao chúng ta cần nhập chữ cái thay vì số và có cần thiết không? Và chỉ sau này bạn mới thấy đại số mang lại lợi ích gì khi giải các bài toán so với số học.

Đại số được sử dụng trong nhiều khoa học chính xác. Đây là vật lý, cơ học, sopromat, điện. Luật Ohm không có gì khác hơn một phương trình đại số: nó đủ để thay thế các giá trị số của chúng thay vì các chữ cái để tìm ra dòng điện nào sẽ chạy trong tải, hoặc điện trở của một phần của mạch.

Vì vậy, bạn đã làm quen với đại số của số, hoặc với đại số tiểu học. Nhiệm vụ chính và gần như duy nhất là có được câu trả lời cho câu hỏi: X Thế nào là X bằng? Bao nhiêu?

Ở trường trung học, họ nghiên cứu sự khởi đầu của đại số vector. Đại số này về cơ bản khác với đại số sơ cấp. Nó có một bản chất khác nhau của bộ nghiên cứu và các quy tắc hành động khác. Giải phương trình vectơ, chúng ta nhận được trong câu trả lời một vectơ không phải là số bình thường trả lời cho câu hỏi. Bao nhiêu?

Các công thức của đại số vectơ ở nhiều khía cạnh khác với các công thức của đại số sơ cấp. Ví dụ, trong đại số sơ cấp và đại số vectơ có một phép toán cộng. Nhưng nó được thực hiện theo những cách hoàn toàn khác nhau.Việc thêm các số hoàn toàn không giống như việc thêm các vectơ.

Có các đại số khác: đại số tuyến tính, đại số cấu trúc, đại số các vòng, đại số logic, hoặc, điều tương tự, đại số Boolean. Có lẽ bạn đã không nghe thấy tên trong các bài học ở trường. George Boole - nhưng mọi người đều biết tên của một trong những cô con gái tài năng của ông Ethel Voinich (1864 - 1960). Cô đã viết cuốn tiểu thuyết "Gadfly", nói về cuộc đấu tranh cho quyền của người dân Ý.

George Bull được sinh ra ở Anh vào ngày 2 tháng 11 năm 1815. Cả đời ông làm giáo viên toán và vật lý ở trường. Từ hồi ký của học sinh, người ta biết Bul có tầm quan trọng lớn như thế nào đối với sự phát triển khả năng sáng tạo của học sinh. Khi trình bày tài liệu mới, ông đã tìm cách đảm bảo rằng chính các sinh viên của mình đã khám phá lại các công thức và luật nhất định.

Kể cho học sinh về những khó khăn mà các nhà khoa học chắc chắn phải đối mặt khi tìm kiếm sự thật, giáo viên thích lặp lại một sự khôn ngoan của phương Đông: ngay cả ngai vàng Ba Tư cũng không thể mang lại niềm vui cho một người như một khám phá khoa học nhỏ nhất. Buhl không bao giờ mất hy vọng rằng một ngày nào đó sinh viên của mình sẽ thực hiện một khám phá thực sự.

Phạm vi lợi ích khoa học của Buhl rất rộng: ông cũng quan tâm không kém đến toán học và logic - khoa học về luật và các hình thức tư duy. Vào thời đó, logic được coi là một ngành khoa học nhân văn, và nhiều người biết George Boole đã ngạc nhiên về cách các phương pháp nhận thức chính xác vốn có trong toán học và các phương pháp logic mô tả thuần túy có thể cùng tồn tại trong một người.

Nhưng nhà khoa học muốn làm cho khoa học về các định luật và các hình thức tư duy nghiêm ngặt như bất kỳ ngành khoa học tự nhiên nào, nói toán học và vật lý. Đối với điều này, Boule bắt đầu biểu thị không phải là số, như được thực hiện trong đại số thông thường, nhưng các phát biểu, và cho thấy các phương trình như vậy, rất giống với đại số, có thể giải quyết các câu hỏi về sự thật và giả của các phát biểu do con người tạo ra. Thế là đại số Boolean nảy sinh.

Nhưng rất lâu trước khi George Buhl, nhà toán học và triết học người Đức Gottfried Leibniz (1646-1716) lần đầu tiên nảy ra ý tưởng tạo ra một khoa học chỉ định tất cả các khái niệm về lời nói thông tục với các biểu tượng và thiết lập một số đại số mới để kết hợp các biểu tượng này.

Sau khi tạo ra một khoa học như vậy, theo Leibniz, các nhà khoa học và triết gia sẽ ngừng tranh cãi và la hét với nhau, tìm ra sự thật, nhưng họ sẽ cầm bút chì và bình tĩnh nói: Hãy tính toán!

Ngày nay, đại số của logic đã trở thành một phần quan trọng của toán học. Một trong những nhiệm vụ của nó là giải quyết tất cả các loại phương trình, các tỷ lệ số được thay thế bằng các chữ cái. Mỗi bạn, có lẽ, trong suốt cuộc đời bạn đã nhớ cách giải phương trình bậc hai và bậc ba với các hệ số chữ cái. Vì vậy, Boole trong đại số mới của mình đã sử dụng tất cả các công thức và quy tắc này.

Điều mới trong đại số Boolean là các phần tử của tập hợp được nghiên cứu trong đó không phải là số, mà là các câu lệnh. Nếu, khi giải các phương trình đại số thông thường, xác định số nào bằng số X chưa biết, đại số trường tìm câu trả lời cho câu hỏi: Thằng bao nhiêu?

Đại số của logic đang tìm kiếm câu trả lời cho câu hỏi: Đây là câu nói này hay câu đó được biểu thị bằng chữ X đúng không?

Ý nghĩa và nội dung của tuyên bố không đóng vai trò nào ở đây. Mỗi tuyên bố chỉ có thể đúng hoặc sai. Nó không thể là một nửa đúng và một nửa sai. Ví dụ, chúng ta có thể nhớ lại việc ném rất nhiều với một đồng xu.

Chỉ có hai trạng thái đồng xu được xem xét ở đó - đầu hoặc đuôi. Theo thỏa thuận của các bên, đại bàng là CÓ, và đuôi là KHÔNG. Không có điểm trung gian nào khác được tính đến trong lý thuyết xác suất, mặc dù chúng có thể. Một đồng xu lật có thể rơi trên một cạnh, lăn xuống sàn đến chân ghế hoặc bàn và giữ ở vị trí thẳng đứng, hoặc thậm chí rơi vào một khoảng trống rộng trên sàn. (Bằng cách tương tự với các mạch điện, hai tình huống cuối cùng có thể được coi là một sự cố ở dạng tiếp xúc bị cháy).Nhưng vào thời đó, đại số Boolean, than ôi, không được sử dụng rộng rãi.

Claude Shannon đã phát hiện ra một lần nữa đại số Buhl. Năm 1938, khi còn là sinh viên của Viện Công nghệ Massachusetts và Mỹ, Claude trẻ tuổi đã chứng minh rằng đại số Boolean hoàn toàn phù hợp để phân tích và tổng hợp các mạch chuyển tiếp và chuyển mạch.

Với sự trợ giúp của đại số Boolean, rất dễ dàng để tạo ra một mạch điện của một máy hoạt động bằng rơle.Đối với điều này, hóa ra, bạn chỉ cần biết chính xác những gì máy nên làm, đó là, bạn cần phải có một thuật toán cho hoạt động của nó. Vì vậy, nền tảng đã được đặt ra cho lý thuyết về các máy kỹ thuật số hoạt động theo nguyên tắc CÓ hoặc KHÔNG.

Tóm lại, như vậy, là lịch sử của đại số Boolean. Trong các bài viết sau chúng tôi sẽ xem xét các luật cơ bản của nó, các ví dụ về các mạch tiếp xúc thực hiện các luật này. Hãy xem xét giải pháp của những nhiệm vụ được đưa ra ở đầu bài viết.

Tiếp tục bài viết: Đại số Boolean. Phần 2. Các luật và chức năng cơ bản

Boris Aladyshkin